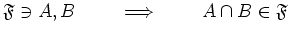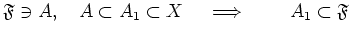ultra filter による極限

DEFINITION 2.1   集合 $X$ の部分集合の族 $\mathfrak{F}$ は 次の条件を満たすとき filter と呼ばれる。

1. $\mathfrak{F} \ni A,B \qquad \implies \qquad A \cap B \in \mathfrak{F}$.
2. $\mathfrak{F} \ni A, \quad A \subset A_1\subset X \quad \implies \qquad A_1 \subset \mathfrak{F}$.

極大な filter のことを ultra filter と呼ぶ。

Ultra filter については次のことが基本的である。

LEMMA 2.2   $\mathcal U$ が集合 $X$ の ultra filter ならば次のことが言える。

1. $X=X_1\cup X_2$ なら、 $X_1$ か $X_2$ のいずれか一方は $\mathcal U$ の 元である。
2. $X=X_1\cup X_2\cup X_3\cup \dots X_N$ なら、 $X_1,X_2,\dots, X_N$ の どれか一つは $\mathcal U$ の元である。
3. 上で、さらに和集合が disjoint union ならば、 $\mathcal U$ の元になる $X_j$ は唯一つのみである。

証明はとてもやさしいので、ここでは省略しよう。 上の補題は $\mathcal U$ が「選択規則」 を与えることをいっている。その意味はあとで少し解説する。

DEFINITION 2.3   $X$ の ultra filter $\mathcal U$ が principal ultra filter であるとは、 ある $x\in X$ があって、

$$\mathcal U= \{ U\subset X; x \in U\}$$

を満たすときに言う。

principal filter は確かに ultra filter ではあるが、 これを考えるならば最初から $X$ の点 $x$ を考えればすむのである。 (Bourbaki は数学原論で principal filter のことを ``trivial filter''と呼んでいるが、その気持ちはよくわかる。)

上の Lemma の(3)から、 つぎのことがすぐわかる。

LEMMA 2.4   集合 $X$ の ultra filter $\mathcal U$ の元 $E$ で、有限集合であるような ものが存在すれば、 $\mathcal U$ は principal filter である。

以下では non-principal ultra filter をおもに考えることになる。