

Next: About this document ...
代数学 II 要約 No.12
上の補題の 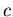 の選びかた。
の選びかた。
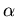 の
の 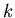 上の共役を
上の共役を
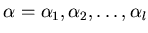 とし、
とし、
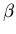 の
の 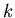 上の共役を
上の共役を
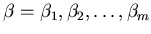 とするとき、
とするとき、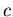 は、
は、
のどれとも異るように選べばよい。
定理 12.1
体
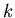
およびその拡大体
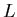
が与えられているとする。
このとき、
は
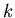
を含む
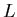
の部分体である。
定義 12.1
体
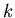
の有限次拡大体
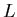
が与えられているとする。
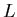
のどの元
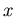
も
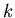
上分離的であるとき、
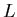
は
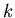
の分離拡大体であるという。
定理 12.2
体
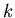
と、その有限次代数拡大体
![$L=k[\alpha_1,\alpha_2,\dots,\alpha_n]$](img18.png)
が与えられているとする。このとき、
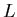
が
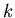
の分離拡大体であるための
必要十分条件は、
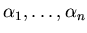
がすべて
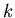
上
分離的であることである。
定理 12.3
無限個の元をもつ体
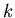
の有限次分離拡大体
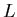
は必ず単純拡大体である。
正規拡大で、かつ分離拡大であるものを、ガロア拡大という。
定理 12.4
体
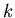
と、その有限次ガロア拡大体
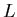
が与えられているとする。
このとき、
がなりたつ。
(注意)
一般に、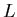 が
が 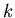 の単純拡大ならば、
の単純拡大ならば、
が成り立つのであった(定理 8.1)。
実は、この不等式は 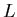 が
が 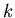 の単純拡大でなくとも、いつでも成り立つ。
問題12.3を参照のこと
の単純拡大でなくとも、いつでも成り立つ。
問題12.3を参照のこと
問題 12.4
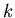
の有限次拡大体
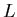
が、
をみたすならば、
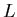
は
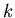
のガロア拡大であることを示しなさい。


Next: About this document ...
Yoshifumi Tsuchimoto
2000-07-03
![]()
![]() の選びかた。
の選びかた。
![]() の
の ![]() 上の共役を
上の共役を
![]() とし、
とし、
![]() の
の ![]() 上の共役を
上の共役を
![]() とするとき、
とするとき、![]() は、
は、
![]()
![]() が
が ![]() の単純拡大ならば、
の単純拡大ならば、