


Next: About this document ...
代数学特論 II 要約 No.6
今日のテーマ:

体 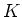 が与えられているとき、正の整数
が与えられているとき、正の整数 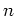 に対して
に対して
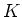 のなかで
のなかで 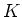 の単位元
の単位元 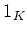 の
の
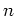 個の和
個の和
を考える。 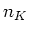 は誤解の恐れのない時には単に
は誤解の恐れのない時には単に 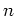 と書かれる。
注意すべきなのは、整数として
と書かれる。
注意すべきなのは、整数として 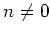 でも
でも 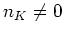 とは限らないこと
である。
とは限らないこと
である。
定義 6.1
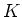
に対して、
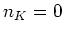
となる最小の正の整数が存在すれば、それを
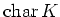
と書き、体
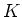
の標数と呼ぶ。
そのような整数が存在しない場合には
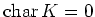
と定義する。
例
素数
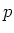
に対して、
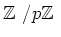
は体であり、その標数は
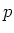
である。
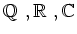
など、
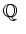
を部分体として含む体は標数
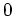
である。
補題 6.1
体の標数は必ず素数かまたは
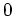
である。
つぎの補題は標数 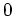 の有限次代数拡大に対しては必ず前回、前々回述べたような
扱いが可能であることを示している。
の有限次代数拡大に対しては必ず前回、前々回述べたような
扱いが可能であることを示している。
補題 6.2
体
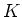
の標数が
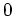
ならば、
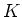
の任意の有限次代数拡大
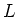
は
単純拡大である。
次の補題は扱っている体に関係なく成り立つが、
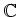 上の代数多様体の関数体の場合には幾何学的に理解できる。
上の代数多様体の関数体の場合には幾何学的に理解できる。
補題 6.3
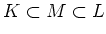
を満たす三つの体
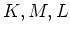
が
与えられているとき、等式
がなりたつ。
問題 6.2
上の問題で、
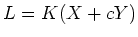
となるような
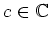
の例を
(補題
6.2 の証明を参考に)一つあげなさい。
2001-11-05
![]()
![]() が与えられているとき、正の整数
が与えられているとき、正の整数 ![]() に対して
に対して
![]() のなかで
のなかで ![]() の単位元
の単位元 ![]() の
の
![]() 個の和
個の和
![]() の有限次代数拡大に対しては必ず前回、前々回述べたような
扱いが可能であることを示している。
の有限次代数拡大に対しては必ず前回、前々回述べたような
扱いが可能であることを示している。![]() 上の代数多様体の関数体の場合には幾何学的に理解できる。
上の代数多様体の関数体の場合には幾何学的に理解できる。