一次従属性

$$e_{\text{牛乳}}= \begin{pmatrix} 0 \\ 10 \\ 0 \\ 1 \end{pmatri... ...matrix}, e_{\text{粉ミルク}}= \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}$$

のあいだには、

$$e_{\text{牛乳}}=10 e_{\text{水}}+e_{\text{粉ミルク}}$$

という関係がある。これは、もちろん、牛乳を 1だけ増やすことが 水10mg と粉ミルク1mg増やすことが同等であることを 言っていて、このような関係があると、 「材料の数」は実質的に2つに減ってしまう。

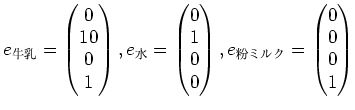
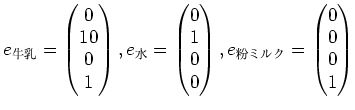
このことを、 $e_{\text{牛乳}}$ は $e_2,e_4$ に一次従属であると表現するわけである。

もっと一般的に言うと、ベクトル $v_1$ がほかの2つのベクトル $v_2,v_3$ に 一次従属であるとは、

$$v_1 = c_2 v_2 +c_3 v_3$$

となる実数 $c_2,c_3$ があると定義される。

しかしながら、上のように述べるよりも、3つのベクトル $v_1,v_2,v_3$ が 平等に現れる形で述べるほうが便利なことも多い。 そこで、次のような定義にたどりつく。

定義 2.1   三つのベクトル $v_1,v_2,v_3$ が一次従属であるとは、

$$c_1 v_1 +c_2 v_2 +c_3 v_3=0$$

を満たすような実数の三つ組 $(c_1,c_2,c_3)$ で、$(0,0,0)$ と異なるものが存在する ときにいう。

上の定義で、 $c_1$ が 0 でなければ、$v_1$ を $v_2$ と $v_3$ の それぞれの定数倍の和(こういうのを線型結合という)で表現できるし、 $c_1$ が 0 でも $c_2$,$c_3$ のどちらか一方が 0 ではないから、 $v_2$ か $v_3$ のいずれかが他の二つのベクトルの線型結合で 書けるわけだ。

ベクトルの数が増えても原理は同じである。念のために定義を書いておくと、 次のようになる。

定義 2.2   $k$ 個のベクトル $v_1,v_2,\dots,v_k$ が一次従属であるとは、

$$c_1 v_1 +c_2 v_2 +c_3 v_3+\dots c_k v_k=0$$

をみたすような実数の $k$ 個の組 $(c_1,c_2,\dots,c_k)$ で、 $(0,0,0,\dots,0)$ と異なるものが存在する ときにいう。

$k$ 個のベクトルが一次従属ではない時、これらは一次独立であるという。