気温ベクトル空間

今度は日本列島各地の気温について考えてみる。 ある特定の時刻を考えると、各地の気温は一意的に決まる。

2002年10月18日の午後1時の気温と言えば、

$$\begin{pmatrix} \text{札幌}\\ \text{新潟}\\ \text{仙台}\\ \tex... ...屋}\\ \text{高松}\\ \text{福岡}\\ \text{鹿児島}\\ \text{那覇} \end{pmatrix}$$

の各成分をそれぞれ決めることができるわけだ。 気温をただ足すことにはそれほど意味はないが、今日の平均気温とか、 一年を通じた平均気温と言う場合には、これらを足して、然るべき数で 割ることになる。つまり、和と、スカラー倍はこれらのベクトルを 考える際にも基本的である。 かくして 「札新仙東名高福鹿那空間」を作ることができる。 ここまでは前までの話と変わらない。

問題は、日本の各地の気温、といった場合、 「札新仙東名高福鹿那」のみでは不十分である、というところにある。 例えば高知も抜けている。各都道府県の県庁所在地ということになると47次元の ベクトル空間を考えねばならない。

ではそれで十分か、と言うともちろんそうではなくて、 高知県でも東部、西部、中央の天候は大きく異なっているし、山間部では やはり少し気温が低いだろう。

ありとあらゆる地点に対するその地点の気温を全部考えると、 次のようなベクトルが出来上がることだろう。

$$\begin{pmatrix} \vdots\\ \text{札幌の気温}\\ \vdots\\ \text{高... ...\\ \text{室戸の気温}\\ \vdots\\ \text{足摺の気温}\\ \vdots\\ \end{pmatrix}$$

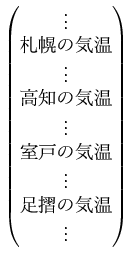
これは、結局、 $J=\{$日本の各地点$\}$ の上の関数

$$J\ni x\mapsto x$$    の気温

を考えているのと同じになる。

この考えをもっと押し進めると、$J$ 上の実数値関数全体 $F(J)$ に 和とスカラー倍を

$$(f+g)(x)=f(x)+g(x),\quad (c f )(x)=c f(x) \qquad (f,g\in F(J), c\in$$   $$\mbox{${\mathbb{R}}$}$$$$)$$

で定義して、ベクトル空間を作ることを思い付くことができるだろう。

上のように式で書かれるとビビルかも知れないが、要するに各地点でそれぞれ 和やスカラー倍を考えなさい、と言っているのであるから、よくよく考えれば 実にやさしいことを言っているのである。