

: 行と列の区別の覚え方
: その2:行列のブロック区分け
: 行列の積を行列と列ベクトルの積に分解する。
ここまでくれば、行列の列基本変形を理解するのはたやすい。
ここでは簡単のため 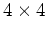 -行列を扱うが、サイズが変わっても同様である。
-行列を扱うが、サイズが変わっても同様である。
四次元縦ベクトル
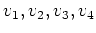 を並べた行列
にたいして、
を並べた行列
にたいして、
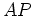 の列ベクトルがどうなるか見てみよう。そのまま計算してもたいしたことは
ないが、やはり基本ベクトルの行き先を見たほうが楽である。
の列ベクトルがどうなるか見てみよう。そのまま計算してもたいしたことは
ないが、やはり基本ベクトルの行き先を見たほうが楽である。
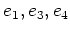 の行き先はやさしい。
の行き先はやさしい。
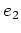 の行き先だけが
の行き先だけが 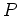 によって味付けされる。
つまり、
となって、
によって味付けされる。
つまり、
となって、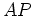 は
は 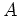 の二列目だけを(二列目+一列目)に変更した
行列になっている。
の二列目だけを(二列目+一列目)に変更した
行列になっている。
このように、行列の基本変形が、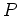 のような行列による
かけ算と対応していることが大切である。
のような行列による
かけ算と対応していることが大切である。
このことを参考にしながら、教科書の列基本変形の項を読んでみよう。
平成15年1月30日
![]() -行列を扱うが、サイズが変わっても同様である。
-行列を扱うが、サイズが変わっても同様である。
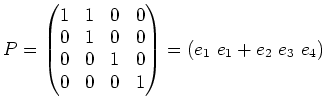
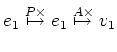
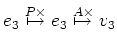
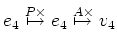
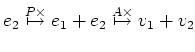
![]() のような行列による
かけ算と対応していることが大切である。
のような行列による
かけ算と対応していることが大切である。