

Next: Schur's lemma
Up: Representations of Weyl algebras
Previous: differential operators in positive
By translating the irreducible representation 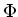 in the previous section,
we obtain a family of irreducible representations.
in the previous section,
we obtain a family of irreducible representations.
Then from what we have shown in the previous section, we obtain the
following results.
LEMMA 7.6
Let
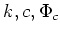 as in Lemma above. Then:
as in Lemma above. Then:
- The kernel of
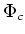 is given as
is given as
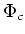 gives rise to a
gives rise to a 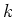 -algebra isomorphism
-algebra isomorphism
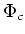 is an irreducible representation of
is an irreducible representation of 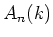 .
.
2007-04-20