実数の集合の例

定義 1.2   実数 $a,b$ について、閉区間 $[a,b]$ と開区間 $(a,b)$ を つぎの式で定める。

$$[a,b] =\{x \in \mbox{${\mathbb{R}}$} \vert a\leq x \leq b\}$$

$$(a,b) =\{x \in \mbox{${\mathbb{R}}$} \vert a < x < b\}$$

◎ $[a,b]$ には端点があって、そこでのようすは $[a,b]$ のほかの点の ようすと大きく異っている。それに対して、$(a,b)$ の各点はどの点も似ている。

◎ $[a,b]$ には最大元があるが、$(a,b)$ にはない。 次の定義を見よ。

定義 1.3   実数 $x$ に対して、その絶対値 $\vert x\vert$ を次のように定義する。

$$\vert x\vert= \sqrt{x^2} = \begin{cases}\phantom{-} x & \text{ if } x\geq 0\ -x & \text{ if } x< 0\ \end{cases}$$

(ただし平方根は0以上のほうを選ぶ。)

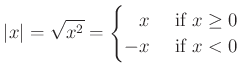上の平方根を使う定義は次のように 高次元の空間にも容易に拡張できるという長所を持つ。 (ただし、「平方根」を用いるのはしばらくは禁じ手であったので これらの平方根を用いた方の定義は平方根の定義を正しく与えるまでは「保留」という事になる。)

$$\vert\vert(x_1,x_2,\dots,x_n)\vert\vert=\sqrt{x_1^2+x_2^2+x_3^2+\dots + x_n^2}$$

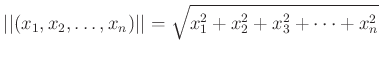
次に出てくる三角不等式も実は高次元の場合にも成り立ち、 解析学の基本的な道具として大切である。

定理 1.4   次の不等式が成り立つ。

1. $x\in$   $\mbox{${\mathbb{R}}$}$ に対して、 $-\vert x\vert \leq x \leq \vert x\vert$ .
2. (三角不等式) $x,y\in$   $\mbox{${\mathbb{R}}$}$ に対して、 $\vert x+y\vert \leq \vert x\vert+\vert y\vert.$

○収束の定義 ($\epsilon$ -$N$ -論法)

定義 1.5   数列 $\{a_n\}_{n=1}^\infty$ が $a$ に収束するとは、

$$\forall \epsilon >0 \exists N$$    such that $$\quad (\forall n>N \quad \vert a_n -a\vert<\epsilon)$$

のときにいう。

問題 1.1   次のうち、正しいものには証明を、間違っているものには反例を述べよ。

1. $\forall \epsilon>0 \exists \delta>0$$\quad\text {such that} (\epsilon>\delta)$ .
2. $\exists \delta >0$    such that $\forall \epsilon>0 (\epsilon>\delta)$ .
3. $\exists \delta \in {\mbox{${\mathbb{Z}}$}}_{>0}\forall \epsilon \in {\mbox{${\mathbb{Z}}$}}_{>0}$ such that $(\epsilon\geq \delta)$ .