Next: stalk of a presheaf Up: , , and the Previous: example of presheaves and
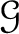 be a presheaf on a topological space
be a presheaf on a topological space 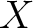 .
Then there exists a sheaf
.
Then there exists a sheaf
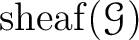 and a presheaf morphism
and a presheaf morphism
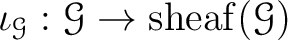
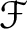 with a presheaf morphism
with a presheaf morphism
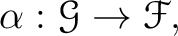
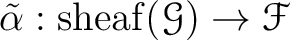
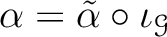
Furthermore, such
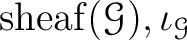 is unique.
is unique.
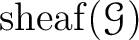 (together with
(together with
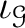 )
is called the sheafication of
)
is called the sheafication of
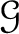 .
.The proof of Lemma 7.28 is divided in steps.
The first step is to know the uniqueness of such sheafication. It is most easily done by using universality arguments. ([#!Lang1!#] has a short explanation on this topic.)
Then we divide the sheafication process in two steps.
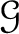 be a presheaf on a topological space
be a presheaf on a topological space 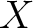 .
Then for each open set
.
Then for each open set
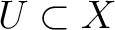 ,
we may define a equivalence relation on
,
we may define a equivalence relation on
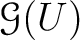 by
by
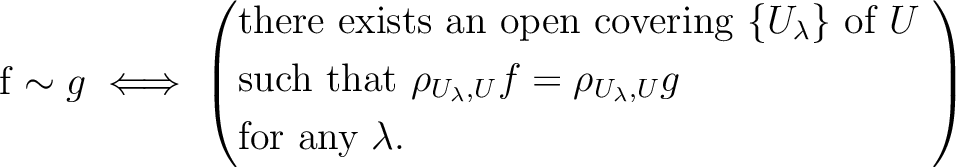
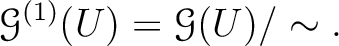
 is a presheaf that satisfies the locality axiom
of a sheaf. There is also a presheaf homomorphism from
is a presheaf that satisfies the locality axiom
of a sheaf. There is also a presheaf homomorphism from
 to
to
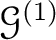 . Furthermore,
. Furthermore,
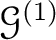 is universal among such.
is universal among such.
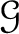 be a presheaf on a topological space
be a presheaf on a topological space 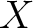 which
satisfies the locality axiom of a sheaf. Then we define a presheaf
which
satisfies the locality axiom of a sheaf. Then we define a presheaf
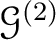 in the following manner.
First for any open covering
in the following manner.
First for any open covering
 of an open set
of an open set
 ,
we define
,
we define
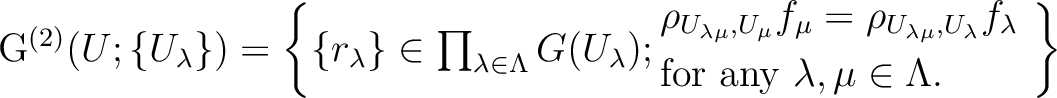
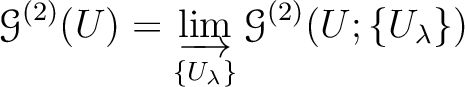
 is a sheaf and that there exists a
homomorphism from
is a sheaf and that there exists a
homomorphism from 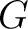 to
to  .
Furthermore,
.
Furthermore, 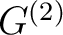 is universal among such.
is universal among such.
Proofs of the above two lemma are routine work and are left to the reader.
Finish of the proof of Lemma 7.28: We put
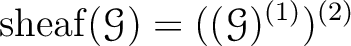
ARRAY(0x55bdfc9e5b40)