|
|
|||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| 研究紹介 | ||||||||||||||||||||||||||
| 3次元トポロジー | ||||||||||||||||||||||||||
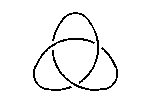
トポロジー(位相幾何学)は現代幾何学の一分野である。古典幾何学では距離や角度の概念が重要な役割を果たしたが,トポロジーはゴム膜の幾何学とも呼ばれ,ある種の連続的な変換で不変な,距離や角度に依存しない図形の性質を調べる学問である。例えば右図の結び目がゴムでできていると考えたとき,どちらの結び目を変形しても,平面に押し込むことはできない。つまり,これらの結び目と平面上の円周は異なるものとして扱われる。 |
 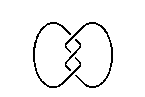 |
|||||||||||||||||||||||||
| 私の研究分野は3次元空間を扱う3次元トポロジーである。3次元空間といってもユークリッド空間とは限らない。私たちは普段の生活の中で,視覚により距離や方向,位置関係などを認識しているが,実際には網膜に映し出された平面画像から3次元空間を復元している。 したがって,3次元空間には一見しただけでは理解できない難しさが潜んでいる。下図 の二つの結び目は平面上に描かれたものだから、ちょうど網膜上の映像と同じ状態になっており,3次元空間内の姿を想像することができるだろう。しかし、これらが同じ結び目を別の視点から描いたものだと理解するには、空間的な変形操作に想像力を働かせる必要がある。 | ||||||||||||||||||||||||||
| 結び目理論 | ||||||||||||||||||||||||||
結び目というと一般的には靴紐などを結んでできるものを想像することが多いが,数学では端点をもたない閉曲線を指している。言いかえると,1次元空間である円周を3次元空間に結ばれた状態で埋め込んだものである。結び目理論はトポロジーの一分野であるが,物理学や化学,生物学と関連があり,結び目を含む化学構造も数多く知られ,DNA結び目というものも発見されている。結び目理論には,代数的なアプローチによる不変量の研究や,対称性のような幾何的性質の研究など様々な分野がある。 |
||||||||||||||||||||||||||
| 3次元多様体上の有限群作用 | ||||||||||||||||||||||||||
私たちは地球という球体の表面で生活しているので,球面上にいると考えられる。しかし,私たちの周囲を見回すだけなら,この球面の一部をユークリッド平面と見なしてもよいだろう。つまり,球面は局所的にユークリッド平面と見なすことができる。同様に他の曲面も局所的にユークリッド平面と見なすことができる。この考え方は3次元の場合にも適用できる。3次元多様体は局所的にユークリッド空間と見なせる3次元空間である。3次元多様体上の有限群作用は,3次元多様体の対称性を表現するものである。結び目の外部空間は3次元多様体になっており,それを調べることは結び目理論に深く関係している。 |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||