



Next: Bibliography
Up: multidegree monoids and lattices
Previous: multidegree monoids and lattices
Contents
Lemma 19
Let

be a field.
Assume
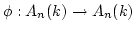
is injective
(which is always the case if
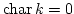
).
Then
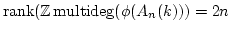
.
Let  be the maximum of total degrees of elements
be the maximum of total degrees of elements
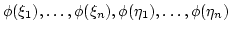 .
Then we see that
.
Then we see that
holds for any 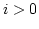 .
Thus for any
.
Thus for any 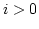 , we have
This together with Lemma 18 gives the result.
, we have
This together with Lemma 18 gives the result.
Lemma 20
Let
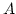
be a subalgebra of a polynomial algebra
![$ P=k[X_1,X_2,\dots,X_m] $](img331.png)
over a field

.
If there exists an positive integer
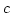
such that
holds for all integers
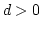
, then we have
Suppose on the contrary that
![$ [Q(P):Q(A)] >c$](img335.png) .
Take elements
.
Take elements
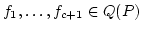 which are linearly independent over
which are linearly independent over 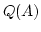 .
By multiplying a ``common denominator'', we may assume that
.
By multiplying a ``common denominator'', we may assume that 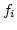 are
elements of
are
elements of 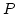 .
Then it follows that the sum
.
Then it follows that the sum
is direct in 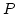 .
Let
.
Let 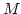 be the maximum of total degrees of
be the maximum of total degrees of
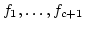 .
Then the directness above implies that an inequality
holds for any integer
.
Then the directness above implies that an inequality
holds for any integer 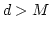 .
Since the left hand side is not greater than
.
Since the left hand side is not greater than
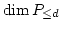 ,
we obtain the following inequation
which leads to a contradiction when
,
we obtain the following inequation
which leads to a contradiction when 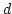 is large enough.
is large enough.
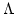
The first statement is an easy consequence of
Lemma 19.
This in turn implies (2) (except for finite primes).
In precise, let
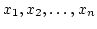 be elements in
be elements in
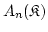 such that
multi degrees of
such that
multi degrees of
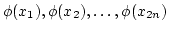 are linearly
independent.
Then for almost all primes,
their reductions
are linearly
independent.
Then for almost all primes,
their reductions
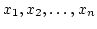 are defined as elements of
are defined as elements of
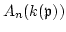 and
their multi degrees stays invariant under the reduction.
and
their multi degrees stays invariant under the reduction.
We apply Lemma 18 to see that
there exists a positive real number 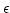 which is independent of
which is independent of
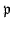 such that an inequality
such that an inequality
holds for any large integer 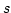 .
.
(1) is already proved in subsection 3.1.
To prove (4), we denote by
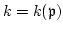 the quotient field with characteristic
the quotient field with characteristic
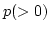 .
Since
.
Since  is a free
is a free 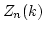 -module of rank
-module of rank 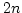 with generators
with generators
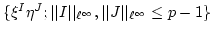 , we have
, we have
Then Corollary 7 gives us an relationship of total degrees
of both hands sides. Namely, there exists a positive number 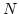 such that
holds for any positive integer
such that
holds for any positive integer 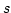 .
.
Combining these, we obtain
Then we use Lemma20 to see that (4)
is true.
(One should be very careful about grading of 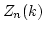 here.
degrees of generators
here.
degrees of generators
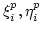 of
of 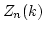 are all
are all 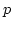 . not
. not 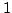 .)
(3) follows from (4) and a consideration on transcendence degrees.
.)
(3) follows from (4) and a consideration on transcendence degrees.
ARRAY(0x8f0db98)ARRAY(0x8f0db98)ARRAY(0x8f0db98)




Next: Bibliography
Up: multidegree monoids and lattices
Previous: multidegree monoids and lattices
Contents
2003/3/3
![]() be the maximum of total degrees of elements
be the maximum of total degrees of elements
![]() .
Then we see that
.
Then we see that
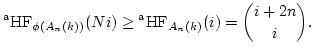
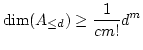
![]() .
Take elements
.
Take elements
![]() which are linearly independent over
which are linearly independent over ![]() .
By multiplying a ``common denominator'', we may assume that
.
By multiplying a ``common denominator'', we may assume that ![]() are
elements of
are
elements of ![]() .
Then it follows that the sum
.
Then it follows that the sum
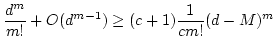
![]() has
rank
has
rank ![]() .
Furthermore, for almost all prime ideals
.
Furthermore, for almost all prime ideals
![]() of
of
![]() ,
we have the following facts.
,
we have the following facts.
![]() which is independent of
which is independent of
![]() such that an inequality
such that an inequality
![]() the quotient field with characteristic
the quotient field with characteristic
![]() .
Since
.
Since ![]() is a free
is a free ![]() -module of rank
-module of rank ![]() with generators
with generators
![]() , we have
, we have
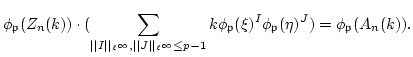
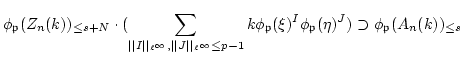
![]()