


: ultra filter による標数 0
: Weyl algebra
: Weyl algebra
標数 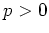 の体
の体 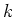 を考える。
簡単のため、
を考える。
簡単のため、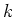 は完全体であると仮定しよう。
Weyl 環の
は完全体であると仮定しよう。
Weyl 環の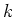 -代数としての自己準同型があると、
それは中心
-代数としての自己準同型があると、
それは中心 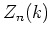 の
の 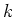 -代数自己準同型を定める。
(このことは自明ではない。
詳しくは [6]に
書いたのでそちらを御参照頂きたい。)
さらに、
-代数自己準同型を定める。
(このことは自明ではない。
詳しくは [6]に
書いたのでそちらを御参照頂きたい。)
さらに、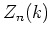 の「
の「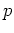 -乗根」を
とすると、
-乗根」を
とすると、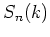 上の
上の
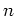 -次元(自明)ベクトル束の接続
-次元(自明)ベクトル束の接続  を
を 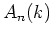 から定めることが
できる。
次の命題が成り立つ。
から定めることが
できる。
次の命題が成り立つ。
PROPOSITION 4.2
[
7]
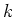
は標数
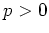
の体であるとする。
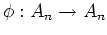
なる
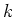
-代数準同型が与えられているとする。
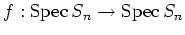
を
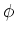
に付随して決まる
morphism とする。
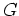
で「ゲージ変換」をあらわすと、
つぎのような等式が成り立つ。
|
(4.1) |
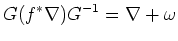 |
ここに、
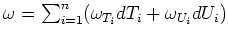
はつぎの微分方程式の一意的な解である。
where
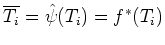
,
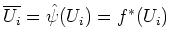
上の命題で、
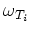 や
や
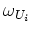 となっているのは
「
となっているのは
「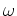 の
の 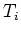 や
や 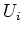 の偏微分」と言う意味ではない。
単に、
の偏微分」と言う意味ではない。
単に、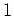 -形式
-形式 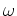 の成分を区別するための suffix である。
物理では時おり見掛けるが、すこしよくない記号だったかも知れない。
(かと言って他によい記号法は見当たらないようにも思える。)
の成分を区別するための suffix である。
物理では時おり見掛けるが、すこしよくない記号だったかも知れない。
(かと言って他によい記号法は見当たらないようにも思える。)
上の命題の微分方程式が面白い微分方程式で、これは例えば 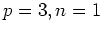 で
で
で定まる 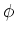 についても使える。
実はこの
についても使える。
実はこの 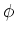 に対する
に対する 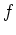 は etale ではなく、上の微分方程式を得る前には
このような例がどのぐらいあるのかわからなかった。
は etale ではなく、上の微分方程式を得る前には
このような例がどのぐらいあるのかわからなかった。
微分方程式が得られたあとでは、次数の関係を吟味することにより、
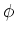 の(多項式としての)次数が
の(多項式としての)次数が 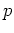 より十分小さければ、
より十分小さければ、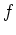 は etale で、
なおかつ 接続
は etale で、
なおかつ 接続  は保存される。
すなわち、Weyl 環にたいして
は保存される。
すなわち、Weyl 環にたいして  を対応させるやり方は、
を対応させるやり方は、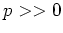 なら
「標準的」であると言ってよい。
この 接続 の曲率は
なら
「標準的」であると言ってよい。
この 接続 の曲率は
である。
平成17年5月17日
![]() や
や
![]() となっているのは
「
となっているのは
「![]() の
の ![]() や
や ![]() の偏微分」と言う意味ではない。
単に、
の偏微分」と言う意味ではない。
単に、![]() -形式
-形式 ![]() の成分を区別するための suffix である。
物理では時おり見掛けるが、すこしよくない記号だったかも知れない。
(かと言って他によい記号法は見当たらないようにも思える。)
の成分を区別するための suffix である。
物理では時おり見掛けるが、すこしよくない記号だったかも知れない。
(かと言って他によい記号法は見当たらないようにも思える。)
![]() で
で
![]() の(多項式としての)次数が
の(多項式としての)次数が ![]() より十分小さければ、
より十分小さければ、![]() は etale で、
なおかつ 接続
は etale で、
なおかつ 接続 ![]() は保存される。
すなわち、Weyl 環にたいして
は保存される。
すなわち、Weyl 環にたいして ![]() を対応させるやり方は、
を対応させるやり方は、![]() なら
「標準的」であると言ってよい。
この 接続 の曲率は
なら
「標準的」であると言ってよい。
この 接続 の曲率は