

: 基本ベクトル以外のベクトルへのかけ算
: その1:基本列ベクトル
: 体や環に新しく元を付け加えて環を作る。(上級者向け)
前小節で 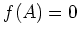 であると述べたが、詳しくは説明しなかった。
ここではその説明を補足することにする。
であると述べたが、詳しくは説明しなかった。
ここではその説明を補足することにする。
まず、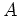 の列ベクトルを眺めてやると、
の列ベクトルを眺めてやると、
が直ちにわかる。
第一式から帰納的に
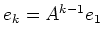 が得られることに注意すると、
が得られることに注意すると、
が成り立つことがわかる。
これらの式を眺めてやると、
右辺をうまく加減してやってうまく消せることに気づくだろう。すなわち、
という関係式が容易に見てとれる。
あとは、
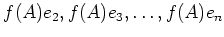 も同様に計算して 0,
とやっても良いのだが、
それではホンマニ同様かいな、という疑念が残る。
も同様に計算して 0,
とやっても良いのだが、
それではホンマニ同様かいな、という疑念が残る。
ここはもっとウマイ手がある。
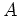 のベキ
のベキ 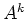 と
と 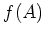 という行列が可換であることを利用するのである。
じっさい、
という行列が可換であることを利用するのである。
じっさい、
とやれば、
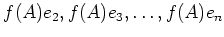 がすべて 0 であることが
ほとんど計算せずにわかるという寸法である。
がすべて 0 であることが
ほとんど計算せずにわかるという寸法である。
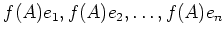 が 0 ならもちろん
が 0 ならもちろん 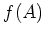 自身が
0 でなければならないから、これで
自身が
0 でなければならないから、これで 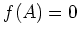 の証明ができたことになる。
の証明ができたことになる。
平成15年1月30日
![]() の列ベクトルを眺めてやると、
の列ベクトルを眺めてやると、
![]() も同様に計算して 0,
とやっても良いのだが、
それではホンマニ同様かいな、という疑念が残る。
も同様に計算して 0,
とやっても良いのだが、
それではホンマニ同様かいな、という疑念が残る。
![]() のベキ
のベキ ![]() と
と ![]() という行列が可換であることを利用するのである。
じっさい、
という行列が可換であることを利用するのである。
じっさい、
![]() が 0 ならもちろん
が 0 ならもちろん ![]() 自身が
0 でなければならないから、これで
自身が
0 でなければならないから、これで ![]() の証明ができたことになる。
の証明ができたことになる。