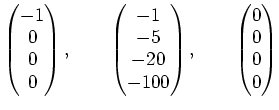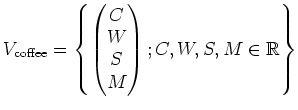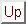

: ベクトル空間の定義の勘どころ
: ベクトル空間の定義
: 初等コーヒベクトル
初等コーヒベクトル全体を集めて来た集合を
「初等コーヒ空間
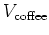 」と呼ぶことにする。
数学ではこのように、「何とか全体を集めて来て集合を作る」のが
常套手段だ。「いまは野球やテニスの話をしているのではなくて、
コーヒの話をしているのですよ。」という風に土俵を決めているとも見ることができる。
」と呼ぶことにする。
数学ではこのように、「何とか全体を集めて来て集合を作る」のが
常套手段だ。「いまは野球やテニスの話をしているのではなくて、
コーヒの話をしているのですよ。」という風に土俵を決めているとも見ることができる。
「全部集めてくる」ということが非常に大事であって、
これを常によく意識しておく必要がある。
ローズさんのコーヒベクトル
とカブレラさんのコーヒベクトル
ももちろん
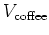 に入っており、そのほかにも、
ありとあらゆる「レシピ」が
に入っており、そのほかにも、
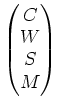
ありとあらゆる「レシピ」が 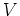 には入っているのである。例えば、
などという、地球上にはあり得ないようなコーヒのレシピも、
には入っているのである。例えば、
などという、地球上にはあり得ないようなコーヒのレシピも、
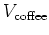 には入っている。(
には入っている。(
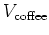 はあらゆる「可能性」あるいは
「紙に書いた(机上の)レシピ」を寄せ集めたようなもので、
それが実現可能かどうかはまた別の問題として扱うのである。)
はあらゆる「可能性」あるいは
「紙に書いた(机上の)レシピ」を寄せ集めたようなもので、
それが実現可能かどうかはまた別の問題として扱うのである。)
先にも述べたように、いろいろなレシピの差も考える必要があるから、
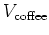 には、
には、
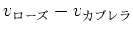 のような、成分に負の数が
入っているようなベクトルも入っていると考える。
もちろん、
のような、成分に負の数が
入っているようなベクトルも入っていると考える。
もちろん、
なども
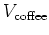 に入っているわけだ。
に入っているわけだ。
つまり、
の 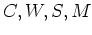 にありとあらゆる実数をいろいろととっかえひっかえ入れてえられる
すべての「コーヒベクトル」を集めたものが
にありとあらゆる実数をいろいろととっかえひっかえ入れてえられる
すべての「コーヒベクトル」を集めたものが
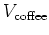 である。
である。
以上のことをいちいち述べていては時間がかかるので、このことを、
と略記する。(セミコロン (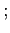 ) のところは縦棒 (
) のところは縦棒 (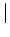 ) にすることもある。)
) にすることもある。)
(上の式を書いた途端に分からなくなったり、変な理解の仕方をしたりする学生を
私は多く知っているけれども、分かってみれば実に単純なことを
言っているのであって、その理解の際には上の例のごとく自分なりの「比喩」を
使えば良いのである。)
初等コーヒベクトルは実数倍したり、2つを足したり、引いたり、できるので、
「コーヒベクトル空間」自体はそのような特別な空間であるといえる。
それが「ベクトル空間」の意味である。
平成15年1月30日
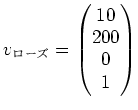
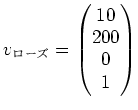
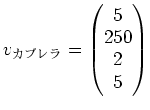

![]() には、
には、
![]() のような、成分に負の数が
入っているようなベクトルも入っていると考える。
もちろん、
のような、成分に負の数が
入っているようなベクトルも入っていると考える。
もちろん、