

Next: 四分割
Up: 平均をとる考え方
Previous: 平均をとる考え方
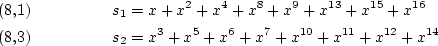
この二つは変換
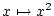 によって不変です.
(``(8,1)'',``(8,3)'')などの記号はガウスが [2] で用いていたものです.
``(8,1)'' は 「
によって不変です.
(``(8,1)'',``(8,3)'')などの記号はガウスが [2] で用いていたものです.
``(8,1)'' は 「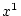 から始めて8つで戻ってくるものを足したもの」
という意味です。以下同様。)
から始めて8つで戻ってくるものを足したもの」
という意味です。以下同様。)
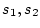 は次の方程式を満たします.
は次の方程式を満たします.
前の式についてはすぐに確かめられます. 後ろの式は単純に展開すると,
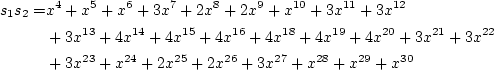
となり, これに 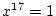 を代入して整理すると,
を代入して整理すると,
という式が得られます.
さらに 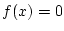 ということから
ということから 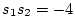 が分かるわけです.
が分かるわけです.
ともあれ, (S)式から 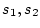 は次のように解けることになります.
は次のように解けることになります.
この複号のどちらを選べばよいかは, 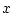 が
が 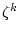 のどれかによって
変わってきます.
のどれかによって
変わってきます.
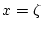 ならば, 数値計算により,
ならば, 数値計算により,
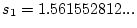 がわかるので,
がわかるので,
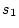 の複号はプラスの方がとられることになります.
の複号はプラスの方がとられることになります.
でもすべてプラス符号です.
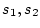 がこうやって求まってみると, (8,1),(8,3)という式は
がこうやって求まってみると, (8,1),(8,3)という式は 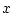 の
16次と14次の方程式を与えることになります.
(あとの議論には必要のないことですが読者の興味のために述べておくと,
この二つからユークリッドの互除法を用いて
の
16次と14次の方程式を与えることになります.
(あとの議論には必要のないことですが読者の興味のために述べておくと,
この二つからユークリッドの互除法を用いて
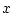 の満たすできるだけ簡単な式を作ることにより,
先に判別式の節で述べたのとまったく同じ式が得られるということが分かります. )
の満たすできるだけ簡単な式を作ることにより,
先に判別式の節で述べたのとまったく同じ式が得られるということが分かります. )
2002-08-15
![]() は次の方程式を満たします.
は次の方程式を満たします.
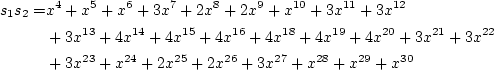
![]() は次のように解けることになります.
は次のように解けることになります.
![]() がこうやって求まってみると, (8,1),(8,3)という式は
がこうやって求まってみると, (8,1),(8,3)という式は ![]() の
16次と14次の方程式を与えることになります.
(あとの議論には必要のないことですが読者の興味のために述べておくと,
この二つからユークリッドの互除法を用いて
の
16次と14次の方程式を与えることになります.
(あとの議論には必要のないことですが読者の興味のために述べておくと,
この二つからユークリッドの互除法を用いて
![]() の満たすできるだけ簡単な式を作ることにより,
先に判別式の節で述べたのとまったく同じ式が得られるということが分かります. )
の満たすできるだけ簡単な式を作ることにより,
先に判別式の節で述べたのとまったく同じ式が得られるということが分かります. )