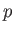 で「中途半端にまわる」のも込めてまわる様子を記述するのが
局所類体論です。まわる様子を記述するのが
Artin map
で「中途半端にまわる」のも込めてまわる様子を記述するのが
局所類体論です。まわる様子を記述するのが
Artin map
で、「何回まわるか」と「中途半端さの度合いは」という問いに対して
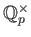 の元で答えます。
以下、岩沢健吉「局所類体論」に沿っています。
(記号を無理やり合わせようとしているため、
他のところと整合性がとれていません。)
の元で答えます。
以下、岩沢健吉「局所類体論」に沿っています。
(記号を無理やり合わせようとしているため、
他のところと整合性がとれていません。)
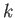 を、標数 0、剰余体の標数が
を、標数 0、剰余体の標数が 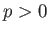 であるような局所体であるとする。
であるような局所体であるとする。
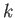 の素元
の素元 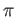 (
(
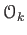 の素元) に対して、次のような
の素元) に対して、次のような
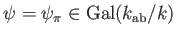 が一意的に存在する。
が一意的に存在する。
| [ |
|---|
l]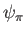 の定義 の定義
|
補題 6.1
群準同型
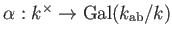 で、任意の素元
で、任意の素元 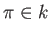 に対して
に対して
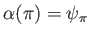 を満たすものが一意に存
在する。
を満たすものが一意に存
在する。
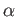 を (local) Artin map と呼ぶ。
を (local) Artin map と呼ぶ。
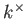 の元
の元 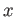 は
は
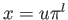
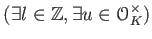 と書かれることに注意します。
と書かれることに注意します。
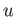 を一つの
を一つの 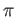 におっつけて
におっつけて
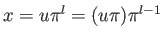 と書きますと、
と書きますと、
 も素元であって、
も素元であって、
と表されます。
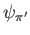 や
や 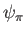 は
は
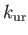 に
制限すると「一回まわる」(Frobenius 写像)に相当しますから、
に
制限すると「一回まわる」(Frobenius 写像)に相当しますから、
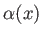 は「
は「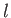 回まわる」のに「イロ(尾ひれ)を付けた」
ようなものだとわかります。
回まわる」のに「イロ(尾ひれ)を付けた」
ようなものだとわかります。
![]() を、標数 0、剰余体の標数が
を、標数 0、剰余体の標数が ![]() であるような局所体であるとする。
であるような局所体であるとする。
![]() の素元
の素元 ![]() (
(
![]() の素元) に対して、次のような
の素元) に対して、次のような
![]() が一意的に存在する。
が一意的に存在する。
![]() の元
の元 ![]() は
は
![]()
![]() と書かれることに注意します。
と書かれることに注意します。
![]() を一つの
を一つの ![]() におっつけて
におっつけて
![]() と書きますと、
と書きますと、
![]() も素元であって、
も素元であって、