
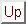

: を実ベクトル空間とみる。
: その1:基本列ベクトル
: 巾零行列
次のような行列を考える
巾零行列の 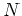 に似てはいるが、左下の
に似てはいるが、左下の 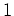 の分だけ様相が異なっている。
この行列による基本ベクトルの行き先を見てみると、
という具合になっている。
これは基底の置換
に対応している。もっと一般に、
の分だけ様相が異なっている。
この行列による基本ベクトルの行き先を見てみると、
という具合になっている。
これは基底の置換
に対応している。もっと一般に、
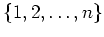 の置換
の置換 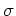 に対して、
それに対応する行列
に対して、
それに対応する行列 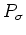 を
が成り立つように定義することができる。
を
が成り立つように定義することができる。
二つの置換
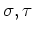 に対して
に対して
だから、
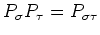 がなりたつことにも注目しよう。
(このような関係式を素早く出せることも、基底の行き先を見ることのご利益である。)
これは置換の乗法構造を行列のそれに置き換えて考える手段をあたえており、
置換群の表現論において基本的な役割を果たす。
がなりたつことにも注目しよう。
(このような関係式を素早く出せることも、基底の行き先を見ることのご利益である。)
これは置換の乗法構造を行列のそれに置き換えて考える手段をあたえており、
置換群の表現論において基本的な役割を果たす。
平成15年1月30日
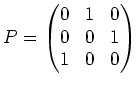
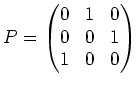
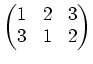
![]() に対して
に対して