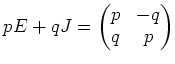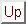

: 体や環に新しく元を付け加えて環を作る。(上級者向け)
: その1:基本列ベクトル
: 置換行列
複素数 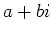 を
を 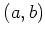 と対応させてみる。
と対応させてみる。
(この対応は全単射であって、しかも、足し算、引き算、実数倍までもが
うまく対応している。つまり 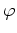 は実ベクトル空間の同型である。 )
は実ベクトル空間の同型である。 )
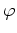 によって、
によって、 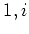 がそれぞれ基本ベクトル
がそれぞれ基本ベクトル 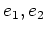 に対応している
ことに注意しよう。
に対応している
ことに注意しよう。
この同型によって 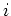 倍するという操作
倍するという操作
は
に対応する。(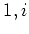 のところを
のところを 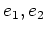 でおきかえただけである。)
この線型写像は行列
であらわされるから、結局 「
でおきかえただけである。)
この線型写像は行列
であらわされるから、結局 「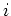 倍する」という作用は
この行列であらわされることになる。
倍する」という作用は
この行列であらわされることになる。
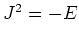 であることにも注意しておこう。これは直接計算で確かめても良いし、
であることにも注意しておこう。これは直接計算で確かめても良いし、
という具合にメノコで確かめてもよい。
同様に、複素数 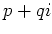 倍するという操作は、
倍するという操作は、
という行列で表現される。
これは複素数を行列で表現する一法である。
平成15年1月30日
![]() を
を ![]() と対応させてみる。
と対応させてみる。
![]() によって、
によって、 ![]() がそれぞれ基本ベクトル
がそれぞれ基本ベクトル ![]() に対応している
ことに注意しよう。
に対応している
ことに注意しよう。
![]() 倍するという操作
倍するという操作
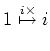
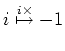
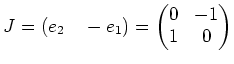
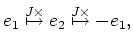
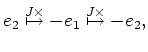
![]() 倍するという操作は、
倍するという操作は、