次の行列 ![]() の行列式を求めよという問題をだした。
の行列式を求めよという問題をだした。
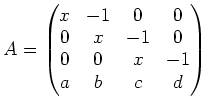
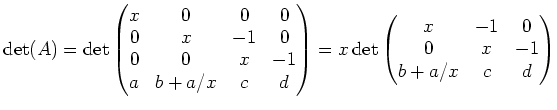 |
||
という具合である。
![]() が何であるか、この問題では指定していないのがミソである。
上の計算では
が何であるか、この問題では指定していないのがミソである。
上の計算では ![]() のときうまくいかない。
だからこのままでは不完全な解答ということになる
7。
のときうまくいかない。
だからこのままでは不完全な解答ということになる
7。
では上の計算方針はダメなのか、というとそうではない。 もう少し言葉を足せば立派な解答になる。
つまり、![]() が変数であると見て、有理式(多項式の分数の形の式)
の範囲内で計算すると、
が変数であると見て、有理式(多項式の分数の形の式)
の範囲内で計算すると、
等しい多項式に何を代入しても等しいから、 ![]() が
変数でなくて、どんな値であっても、両辺は等しい。
つまり
が
変数でなくて、どんな値であっても、両辺は等しい。
つまり ![]() でも上の式は正しい、というわけである。
でも上の式は正しい、というわけである。
結局等しいからどっちでもよい、というわけではない。 上の論法が効かないような場合も往々にしてあって、 その都度考えるのが大事なのである。
考えてみれば、数学の演習というのは気が楽であって、「例外的な場合」を忘れたから といっても、せいぜい先生に怒られたり、単位が足らなかったりするだけである。 飛行機の設計、医療現場など、例外処理がうまくいかないととんでもないことになる 例はいくらでもある。数学はそれらの局面でも使われているわけであるから、 心して問題にあたっていただきたい。
ここで言っておきたいもうひとつのことは、間違いを指摘されてもすぐに消すな、 ということである。上の解答でも、「それでは足りない」と指摘されると、 証拠隠滅とばかりに全部の計算を跡かたもなく消してしまう学生をよく見掛けるのだが、 それでは進歩がない。「あと一歩」というところまで来ているのに、 今まで来た道を全部戻ってしまうようでは、余りにももったいないではないか。
もちろん戻らなければならない時も往々にしてある。しかしそれは じっくり考えてからで十分である。自分の黒板での解答を消す時には、 じっくり考えてから消していただきたい。