![]() の根
の根
![]() の中から二つ
の中から二つ
![]() をとってきてその差
をとってきてその差
![]() をつくり,
それをすべての組合せについて掛け合わせたもの
をつくり,
それをすべての組合せについて掛け合わせたもの
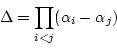
今の場合 ![]() の根の一つを
の根の一つを ![]() とおくと, あとの根はそのベキ乗で
あらわされますから,
とおくと, あとの根はそのベキ乗で
あらわされますから,
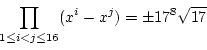
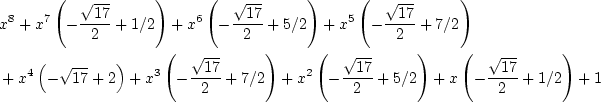
これも, 上から読んでも下から読んでも同じ式(自己相反多項式)ですから,
前小節のやり方と同様にして, この多項式の根を求めることは
2次方程式と4次方程式を解くことに
帰着できます. 当時4次方程式の解き方は知られていましたから, これで
どうにかこうにか ![]() が解けそうです。
が解けそうです。
ただし, これでは初等的には違いないけれども, 計算は大変です. ガウスはもっとずっと簡単な説明をもっていました.