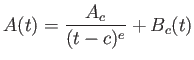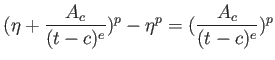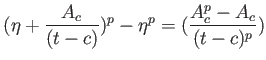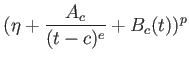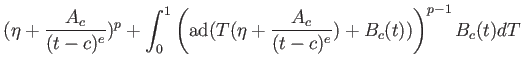一般の場合も、各点
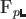 で考えて得られる結論は変わりません。
ただし詳細はわずかに異なるので、
念のためここに書いてみます。
で考えて得られる結論は変わりません。
ただし詳細はわずかに異なるので、
念のためここに書いてみます。
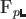 にたいして、
にたいして、
と分解してみます。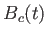 の部分がなければ話は可換の場合になるので、
の部分がなければ話は可換の場合になるので、
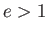 なら、
なら、
「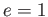 」 ならば、
」 ならば、
なのでした。
Jacobson の公式により、
積分の掛かる項はすべて 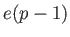 位以下のpoleですから、
結局、
位以下のpoleですから、
結局、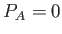 になるためには
になるためには 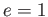 で、
で、
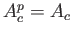 でなければならないことがわかります。
これは
でなければならないことがわかります。
これは 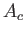 の最小多項式が
の最小多項式が
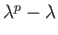 の約数でなければ
ならないことを意味しますから、
の約数でなければ
ならないことを意味しますから、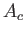 の固有値は
の固有値は
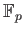 の元で、
なおかつ
の元で、
なおかつ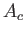 は対角か可能であることがわかります。
まとめると:
は対角か可能であることがわかります。
まとめると:
命題 9.2
ほとんどすべての 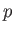 にたいして、
にたいして、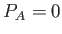 となると仮定すると、
となると仮定すると、
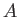 は一位の pole しかもたず、なおかつそれぞれの pole での residue は
有理数である。
は一位の pole しかもたず、なおかつそれぞれの pole での residue は
有理数である。