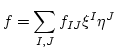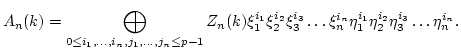-
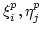 belongs to the center of
belongs to the center of  .
.
- More precisely, the center
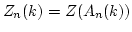 of the ring
of the ring  is given by
is given by
![$\displaystyle Z_n(k)=k[\xi_1^p,\dots,\xi_n^p,\eta_1^p,\dots,\eta_n^p].
$](img108.png)
 is a free
is a free 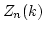 -module of rank
-module of rank 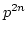 .
.
- Let
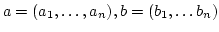 be elements of
be elements of 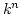 .
Let
.
Let 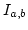 be an ideal of
be an ideal of  generated by
generated by
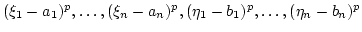 .
Then we have
.
Then we have
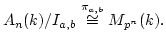
- If the field
 is algebraically closed,
then any maximal (both-sided) ideal of
is algebraically closed,
then any maximal (both-sided) ideal of  is of the form
is of the form 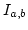 above.
above.