



Next: reduction to characteristic
Up: Preliminaries on Dixmier conjecture
Previous: light exponential function
Contents
For any ring  we denote by
we denote by  the Weyl algebra:
where
the Weyl algebra:
where
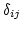 is the Kronecker's delta.
is the Kronecker's delta.
One of the good ways to compute
multiplications of elements in  appears in [2, formula (11,4)].
For any variable
appears in [2, formula (11,4)].
For any variable 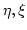 with the canonical commutation relation
with the canonical commutation relation
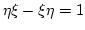 ,and for any pair of ``normally ordered'' polynomials
,and for any pair of ``normally ordered'' polynomials
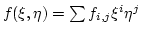 and
and
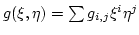 , one has the following formula
, one has the following formula
where 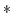 stands for an `multiplication as though
stands for an `multiplication as though 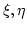 commutes'.
This formula is valid and proved in the book cited above
only if characteristic of the coefficient field is 0.
If the characteristic
commutes'.
This formula is valid and proved in the book cited above
only if characteristic of the coefficient field is 0.
If the characteristic 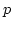 of the coefficient field is positive,
then we replace
of the coefficient field is positive,
then we replace 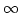 in the above formula by
in the above formula by 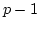 and obtain a
valid formula in this case. The proof is almost the same.
It is well suited for computer calculation using commutative polynomials and
differentiations.
and obtain a
valid formula in this case. The proof is almost the same.
It is well suited for computer calculation using commutative polynomials and
differentiations.
Dixmier conjectures that
Conjecture 1
Every
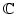
-algebra endomorphism
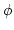
of
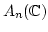
is invertible
(that is, it is an automorphism).
Since
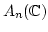 is simple (has no nontrivial both-sided ideal),
we know that
is simple (has no nontrivial both-sided ideal),
we know that 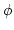 above is injective. The question therefore is
the surjectivity of
above is injective. The question therefore is
the surjectivity of 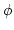 .
.
Subsections




Next: reduction to characteristic
Up: Preliminaries on Dixmier conjecture
Previous: light exponential function
Contents
2003/3/3
![]() appears in [2, formula (11,4)].
For any variable
appears in [2, formula (11,4)].
For any variable ![]() with the canonical commutation relation
with the canonical commutation relation
![]() ,and for any pair of ``normally ordered'' polynomials
,and for any pair of ``normally ordered'' polynomials
![]() and
and
![]() , one has the following formula
, one has the following formula
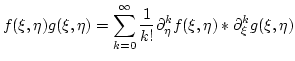
![]() is simple (has no nontrivial both-sided ideal),
we know that
is simple (has no nontrivial both-sided ideal),
we know that ![]() above is injective. The question therefore is
the surjectivity of
above is injective. The question therefore is
the surjectivity of ![]() .
.