



Next: A splitting algebra of
Up: First properties of Weyl
Previous: Weyl algebras over fields
Contents
Lemma 4
Let

be a field of characteristic
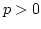
.
For any

-algebra endomorphism
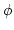
of

,
-
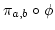 is a surjective homomorphism for all
is a surjective homomorphism for all
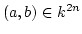 .
.
-
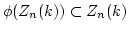 .
.
We may assume that  is an algebraically closed field.
is an algebraically closed field.
(1)
The kernel
of
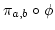 is an ideal of
is an ideal of  and therefore,
by a dimension argument, is one of the maximal ideals of
and therefore,
by a dimension argument, is one of the maximal ideals of  .
It also follows that
.
It also follows that
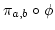 is surjective.
is surjective.
(2)
The result (1) implies that for any
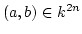 we have
we have
Thus the claim deduces to the following sublemma.
[proof of sublemma]
The left hand side may be identified
with a section of
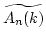 which reduces to 0
at each
which reduces to 0
at each  -valued point
when we regard it as a section of
-valued point
when we regard it as a section of
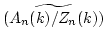 .
Since
.
Since  is an infinite field, this implies that
is an infinite field, this implies that
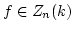 .
.
Corollary 1

is generated by
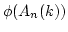
and
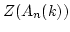
.
[proof]
We may assume  is algebraically closed.
Let
is algebraically closed.
Let 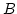 be the algebra generated by
be the algebra generated by
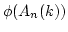 and
and 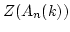 .
Then the claim (1) of the previous lemma
shows that
for any maximal ideal
.
Then the claim (1) of the previous lemma
shows that
for any maximal ideal
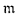 of
of 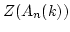 ,
we have an isomorphism
as
,
we have an isomorphism
as 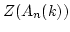 -modules.
Since
-modules.
Since  is finitely generated module over
is finitely generated module over 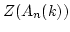 ,
we see immediately that
,
we see immediately that 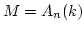 as required.
as required.
Corollary 2
Let
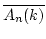
be a copy of

.
Let
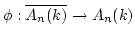
be a

-homomorphism.
Let
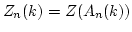
,
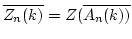
be the center of the algebras

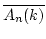
, respectively.
Then the natural homomorphism
is an isomorphism.
By the corollary above we already know that it is surjective.
Since both hand sides are free 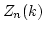 -modules of rank
-modules of rank 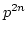 ,
and since
,
and since 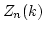 is
an integral domain, the map is a bijection.
[The surjection admits a splitting. Then we consider determinants.]
is
an integral domain, the map is a bijection.
[The surjection admits a splitting. Then we consider determinants.]
Corollary 3
An algebra homomorphism
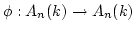
is
surjective if and only if its restriction to the center
is surjective.
By the birational case of the Jacobian conjecture (which is already known
to be true), we conclude that
ARRAY(0x8ec1938)




Next: A splitting algebra of
Up: First properties of Weyl
Previous: Weyl algebras over fields
Contents
2003/3/3
![]() is an algebraically closed field.
is an algebraically closed field.
![]() is an ideal of
is an ideal of ![]() and therefore,
by a dimension argument, is one of the maximal ideals of
and therefore,
by a dimension argument, is one of the maximal ideals of ![]() .
It also follows that
.
It also follows that
![]() is surjective.
is surjective.
![]() we have
we have
![]() which reduces to 0
at each
which reduces to 0
at each ![]() -valued point
when we regard it as a section of
-valued point
when we regard it as a section of
![]() .
Since
.
Since ![]() is an infinite field, this implies that
is an infinite field, this implies that
![]() .
.
![]()