$R$-線型 abel 圏

まず次のような概念を補助的に導入しよう。 (だれでも考えそうな概念であるが、はじめ筆者には 文献が見当たらなかったので、 ``$R$-abel 圏''と呼んでいた。 後に実は $R$-線型 abel 圏として知られていることが わかった。ただ未だに出典がはっきりしない。)

DEFINITION 3.1   可換環 $R$ に対して、 abel 圏 $\mathcal C$ が $R$-線型 abel 圏であるとは、 $\mathcal C$ につぎのような構造が付加されているときに言う。

1. 任意の $M_1,M_2\in \Ob(\mathcal C)$ にたいし、 $\Hom _{\mathcal C}(M_1,M_2)$ は $R$-加群の構造を持つ。
2. $R$-加群の構造は射の合成と協調的である。すなわち、
   $$(a. f) \circ g = a.(f \circ g) = f \circ (a.g)$$
   が任意の $a \in R$ と $\mathcal C$ の(合成可能な) $f,g$ について 成り立つ。

$R$-線型 abel 圏から $R$-線型abel 圏への $R$-線型函手とは、 普通の意味の(additive な)函手で あって、$R$-加群の構造を保つものをいう。

$R$-加群の全体 $(R-$module$)$ はもちろん $R$-線型 abel 圏である。 さらに、$R$-線型 abel 圏 $\mathcal C$ がaugmented であるというのを、 $(R-$module$)$ から $\mathcal C$ への $R$-共変函手が与えられているときに いうことにする。(これは筆者が付け加えた定義である。)

DEFINITION 3.2   $\mathcal C$ は可換環 $R$ 上の $R$-線型 abel 圏であるとする。 $R$ のイデアル $I$ に対して、 $R/I$-線型 abel 圏 $\mathcal C/I$ を、次のような $\mathcal C$ の 充満部分圏として定義する。

$$\Ob(\mathcal C/I)=\{ M \in \Ob(\mathcal C); I M=0\}.$$

( $I M=0$ は実際には圏論的に、「任意の $a\in I$ に対して

$$M \overset{\times a}\to M \qquad$$

が 0 と一致する」と解すべきである。)

DEFINITION 3.3   $k$ は標数 $p \neq 0$ の体であるとする。 「little non commutative algebraic space of finite type (LNCAS) over $k$」 とは、 次のデータをいう。

1. 通常の意味の代数空間 $X$ で、$k$ 上 finite type なもの。
2. $X$ 上の代数層 $\mathcal A$ であって、 $\mathcal A$ は $\mathcal O_X$-加群として $\mathcal O_X$-連接的なもの。

これらのデータを、 $(X,\mathcal A)$ とかく。さらに、 $\mathcal C_\qcoh (X,\mathcal A)$ で、 $\mathcal A$-加群で、 $\O_X$-準連接的であるようなもの全体のなす augmented $k$-線型 abel 圏を表す ことにする。

DEFINITION 3.4   $R$ は、代数体 $\mathfrak{K}$ の整数環 $\mathfrak{O}$ の 有限局所化であるとする。 ``non commutative algebraic space of finite arithmetic type'' $X$ (over $R$) とは、つぎのデータを言う。

1. $R$-線型 abel 圏。これを(象徴的に) $\mathcal C_\qcoh(X)$ とかく。
2. 各極大イデアル $\pe \in \Spm (\mathfrak{O})$ に対して、 ある little non commutative algebraic space of finite type $(X_{(\pe )},\mathcal A_{X(\pe )})$ over $R/\pe$
3. 各 $\pe \in \Spm (\mathfrak{O})$ に対して、 同型 $\mathcal C_\coh/\pe \isoto \mathcal C_\qcoh(X_{(\pe )},\mathcal A_{X(\pe )})$

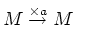
さすがに ``non commutative algebraic space of finite arithmetic type'' という語は長すぎるので、以下では pre NCASと呼ぶことにする。 (``finite arithmetic type'' のところが訳されていないが、これは この文では常に仮定するので省いていると思って頂きたい。)

$R$ 上の pre NCASのあいだの morphism は、 これらのデータと可換になるようなものとして定める。 もっと具体的にいうと、次のようになる (little NC 代数空間の 射は、想像がつくだろう(スキームの射の定義を思い浮かべればよいだろう。) からここでは省略する。)

DEFINITION 3.5   $R$ は、代数体 $\mathfrak{K}$ の整数環 $\mathfrak{O}$ の 有限局所化であるとする。 $X$, $Y$ が $R$ 上のpre NCASであるとき、$X$ から $Y$ への morphism とは データ

1. $\mathcal C_\qcoh(Y)$ から $\mathcal C_\qcoh(X)$ への共変函手 (``引き戻し'').
2. 各 $\pe \in \Spm (\mathfrak{O})$ に対して、 $(X_{(\pe )},\mathcal A_{X(\pe )})$ から $(Y_{(\pe ),A_{Y(\pe )}})$ への LNCASとしての射 $f_{(\pe )}$.

であって、引き戻しと modulo $\pe$ が各 $\pe$ について可換なものをいう。

以上の定義は例を見てはじめて真価がわかる。

可換なものが付随しているので、pre NCASが 「localization, etale, smooth」 などの定義が かなり想像しやすい。

例えば、$X$ が smooth であるとは、各 $\pe \in \Spm (\mathfrak{O})$ に対して、 $X_{(\pe )}$ が smooth で、 なおかつ、 $\mathcal A_{X(\pe )}$ が $X_{(\pe )}$ 上 $\mathcal O_{X(\pe )}$-加群として有限階数の自由加群 であるときに言う、とやればよい。ただしもう少し条件を追加したほうが よいと思われる(例えば、 $X_{(\pe )}$ が $\pe$ によらずに決まるある代数空間 の $\mathfrak{O}/\pe$ に係数を落としたものになっている という条件を課したほうがよいかも知れない等々。) のも確かなので、ここではおくことにする。

pre NCASのなかでも基本的と考えられるのが、affine なもの、すなわち ある $\mathfrak{O}$-代数 $A$ があって、 $\mathcal C_\qcoh(X)$ が ($A$-modules) であるようなものである。

もっとも、どんな $A$ にたいしても $(A-$modules$)$ が pre NCAS になるわけではない。(4.2節) ここで扱いたいのは、微分のなす環や、それに近いもの、なかでも Weyl環(4.1節)や半単純 Lie 環の普遍包絡環 (4.3節)である。

$X_{(\pe )}$ としては、$A/\pe A$ の中心の $\Spec$ を採るのが自然である ようにもみえる。 実際、Weyl 環ではそれでよいのだが、 が、半単純 Lie 環の普遍包絡環の例では そうでもないようである。

もうすこしいろいろな例について研究することが必要であるとおもわれる。

以下では幾つかの例について、アファインな pre NCASとその「貼り合わせ」 のときにどのようなことが起こりそうかを中心に見ることにする。